Mathematics Research
I was a PhD student in mathematics at the University of Oxford under the supervision of Professor Cornelia Druțu. I successfully defended my thesis (On the coarse geometry of solvable Baumslag-Solitar groups and relatively hyperbolic groups) in May 2024.
My field of research was "geometric group theory" which involves applying the techniques and intuition of geometry to problems in algebra and group theory. I was particularly interested in
- Quasiisometric embeddings between groups and metric spaces
- Algorithmic properties of groups such as automaticity
My papers are written under the name Patrick S. Nairne.
Publications and preprints
- Regularity of Quasigeodesics Characterises Hyperbolicity, with Sam Hughes and Davide Spriano, Proceedings of the Royal Society of Edinburgh, 2025
- Embeddings of Trees, Cantor Sets and Solvable Baumslag-Solitar Groups, Geometriae Dedicata, 2023
- Embedding relatively hyperbolic groups into products of binary trees (ArXiv preprint), 2024
- Two new constructions in the theory of projection complexes (ArXiv preprint), 2024
Talks
- Cone types of geodesics and quasigeodesics in groups, Cambridge Junior Geometry Seminar, Cambridge, 1st March 2024
- Quasiisometric embeddings of groups into products of binary trees, GAGTA 2024, Luminy, 5th February 2024
- Regular languages of geodesics and quasigeodesics in groups, PGTC conference, Heriot-Watt University, 13th July 2023
- Obstructions to embeddings between trees, Geometry and Topology Seminar, University of Bristol, 11th October 2022
- Quasiisometric Embeddings of Solvable Baumslag-Solitar Groups, Graduate Student Concentration Week on Metric Geometry, Texas A&M University, July 28th 2022
- QI embeddings of Baumslag-Solitar Groups, Séminaire d'Algèbres d'Opérateurs, Institut de Mathématiques de Jussieu, 2nd June 2022
- Embeddings of Trees and Solvable Baumslag-Solitar Groups, Oxford Junior Topology and Group Theory Seminar, University of Oxford, 27th April 2022
- Quasiisometric Embeddings of Treebolic Spaces, Strukturtheorie Seminar, TU Graz, 4th November 2021
- Asymptotic Cones and the Filling Order of a Metric Space, Oxford Junior Topology and Group Theory Seminar, University of Oxford, 3rd February 2021
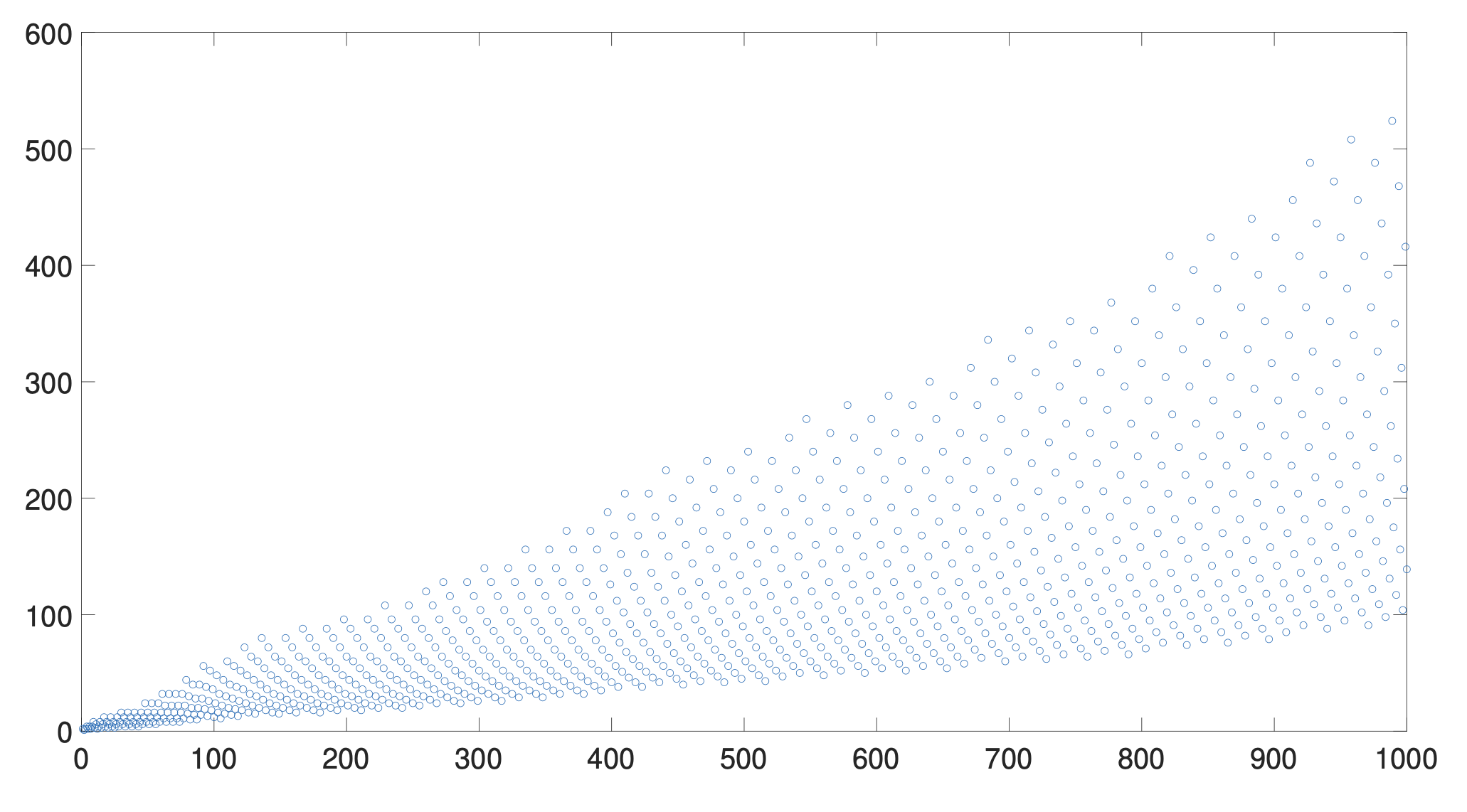
An integer sequence
Imagine that you are about to go for a walk along the number line (a long pebbly beach), beginning at 1 and walking forwards in the positive direction from there.
Suppose that you begin with a single pebble in your hand.
As you walk, you obey the following rule: each time you pass a power of 2, multiply the amount of pebbles in your possession by 2; each time you pass a power of 3, divide your pebbles evenly into 3 groups and keep only one of the larger groups (e.g. divide 8 pebbles into 3,3,2 and then keep only 3 pebbles).
The changing quantity of pebbles in your possession as you walk along the number line forms an integer sequence. The sequence begins
1, 1, 2, 1, 2, 4, 2, 4, 2, 4, 8, 3, 6, 2, 4, 8, 3, 6, 12, 4, ...
The plot belows shows the first 1000 elements of the sequence. For more details you can have a look at my paper Embeddings of Trees, Cantor Sets and Solvable Baumslag-Solitar Groups linked above.